編譯器學習記錄1️⃣：人肉卡西歐計算器

前言：計算器的故事
💪🏻 Motivation
🏁 中級目標
1️⃣ 解析數學式：建立語法樹
2️⃣ 計算數學式：爬樹計算器
3️⃣ 解析數學式：玩弄字符串
展望
註釋

前言：計算器的故事

衆所周知世界上只有兩種計算器，一種是卡西歐函數計算器，另外一種是，😁，其他計算器，，，

俺相信，每個剛踏入初中的小學博士畢業生，在拿到自己的第一臺卡西歐函數計算器之後，都會發出讚歎奇聲如下：

臥草 😆 能直接輸入八百字的數學式
臥草 😨 內置三角函數
臥草 😱 還能定義變量

內置數學式解析功能的神奇計算器，這之後的二十年我拼盡全力無法戰勝……我的水平只能支撐我寫出這種東西 😁：

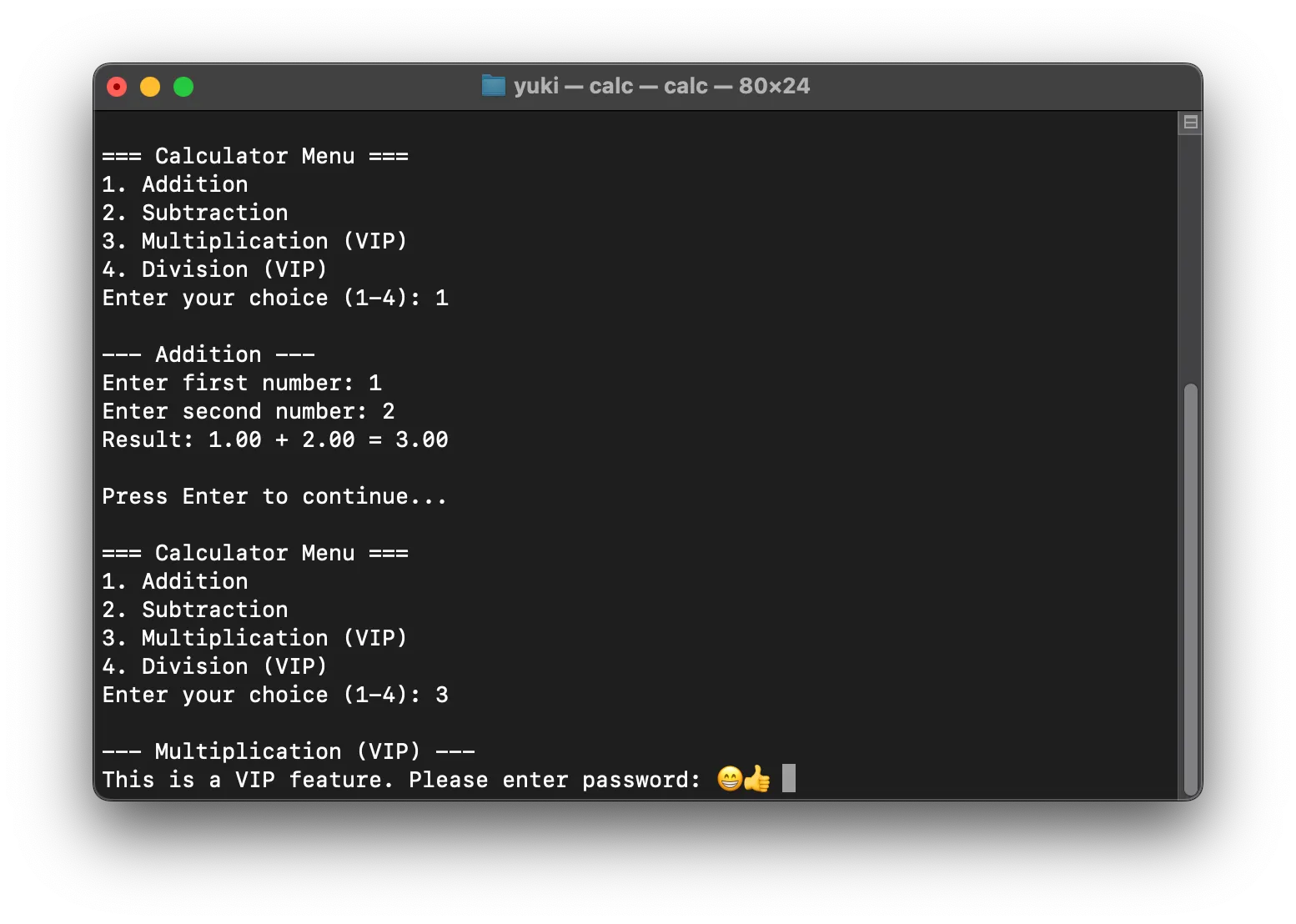
俺的 C++ 還不如大一學生的大作業水平 😆

💪🏻 Motivation

有的羣友可能就要問了，你爲什麼閒着沒事幹要研究計算器甚至編譯器呢？原因是，有一位神必人¹在 👉🏻俺的評論區發表了重要講話，她提到：

逆向工程師的終極必學課程——
是編譯原理和解釋器設計。😰
此話怎講？現代軟件保護技術以及複雜的軟件架構的演進，已經將戰場推向的更高層次的抽象領域。逆向工程師若僅懂彙編與調試器操作，猶如赤手空拳面對鋼鐵堡壘。
虛擬化保護與自定義指令集已經成高強度軟件保護（如遊戲反作弊、金融安全組件）的標配。以頂尖保護殼 VMProtect 為例，其核心技術在於將原始機器碼轉換為自定義字節碼（opcode），並在獨立的虛擬機（VM）中執行。

然後，著名電腦科學家高德納曾經說過：

若觉几乎所有时间都耗于理论，不妨转而关注实践，理论自会因此精进；
若觉几乎所有时间都耗于实践，不妨转而探究理论，实践亦将因此提升。

理論與實踐是相生相伴，螺旋上升的關係。畫畫如此，逆向工程也是一樣。當我發現我的理論知識已經無法支撐我繼續實踐下去，就到了該惡補理論知識的時候了 😰

🏁 中級目標

越來越多的高級語言都需要一個 VM 來執行，比如說 JS 和 Python。並且，幾乎每一個遊戲引擎都內置了一個 VM 用來執行遊戲腳本——所以 VM 無處不在。

我學習 Crafting Interpreters² 的目標就是學會手撕一個自己的 VM，然後……不知正焉知逆！這將爲我拆解別人的 VM 的時候打下堅實的基礎 😎

我仍然記得三年前嘗試手撕 BGI 引擎³遊戲的驗證而空手而歸的感覺 😕 該遊戲的關鍵邏輯並不在 C++ 層面，而是深藏於 VM 執行的腳本之中，對我造成了降维打擊。

1️⃣ 解析數學式：建立語法樹

然而，一步登天是不可能的，搞逆向可不是搞前端，，，

雖然說我可以直接從 VM 和指令的設計開始學，然後直接開逆，不過這會導致俺的知識體系處於一個空中樓閣的狀態。況且，俺也有一個手撕一套屬於自己的語言，編譯器和 VM 的小小願望，這就導致俺必須要從更基礎的，🙀，編譯原理，開始學習。

一說到編譯原理，就有人要提三劍客——龍書，虎書，和鯨書了

這是千千萬程序師窮盡一生都無法企及的高度，我先知難而退了 😁

學習嘛，快樂最重要！沒有快樂就沒有堅持，所以俺決定從輕鬆愉快的部分開始。正好，Crafting Interpreters 前幾章正在講怎麼解析數學式。而編譯的很大一部分步驟都是在解析各種式子和語句，所以，讓我先來輕鬆愉快地實現一個計算器。

考慮一個數學式如下：

1 + 31 * (5.5 + 2) - 4

現在電腦來計算這個長算式了，牠需要一個這樣的數據結構：

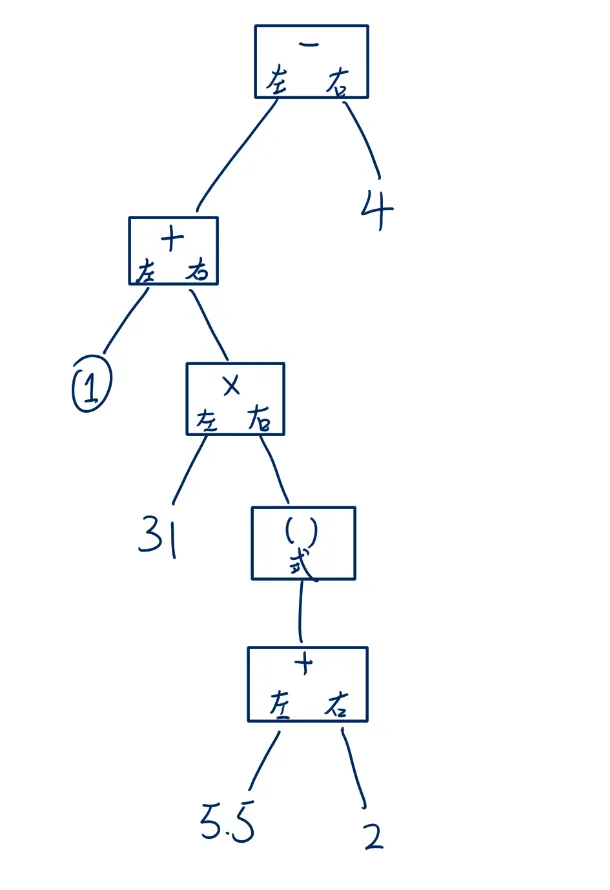
從最頂上開始：

計算一個「減號」，左邊是另外一個「加式」，右邊是 4
要計算第一步的減，先計算那個「加式」，左邊是 1，右邊是一個「乘式」
要計算第二步的加，先計算那個「乘式」，左邊是 31，右邊是一個括號
要計算第三步的乘，先計算括號裏面的「加式」，左邊是 5.5，右邊是 2
第四步的結果是 7.5，括號的結果是 7.5
第三步「乘」的結果是 232.5
第二步「加」的結果是 233.5
第一步「減」的結果是 229.5

最後得到結果是 229.5。
可見，把數學式表示成樹狀結構有兩個好處：

非常易於確定計算的優先順序，
由於上方的計算依賴下方的計算結果，俺們就會把需要優先的括號和乘除放到下方去。
算法簡單，用遞歸實現就是：計算左邊的式，計算右邊的式，計算自己。
每一個式都各自計算自己的左邊和右邊，最後綜合計算結果。

2️⃣ 計算數學式：爬樹計算器

俺敢打包票，每一臺高級卡西歐計算器裏面都用樹狀結構來表示數學式，並且都有遞歸算法來進行求值計算。

就像對於上面那個數學式的計算，我可以這樣實現（僅限加減乘除和括號：

function evaluate(expr: Expr): number {
  if (expr is Literal) {  // 純數字
    return expr.value;
  }
  if (expr is Grouping) {  // 括號
    return evaluate(expr.expression);
  }
  if (expr is Binary) {  // 加減乘除
    const left = evaluate(expr.left);
    const right = evaluate(expr.right);
    switch (expr.operator) {
      case '+': return left + right;
      case '-': return left - right;
      case '*': return left * right;
      case '/': return left / right;
    }
  }
}

除了數學式，編程語言的語法結構也可以塞進語法樹裏面，假設我有這麼一個 JS 代碼：

const a = 42;
function addA(d) {
    return a + d;
}
const c = addA(2) + 5;

那把他裏面的語句一條條組裝在一起，會呈現這樣一個語法樹⁴：

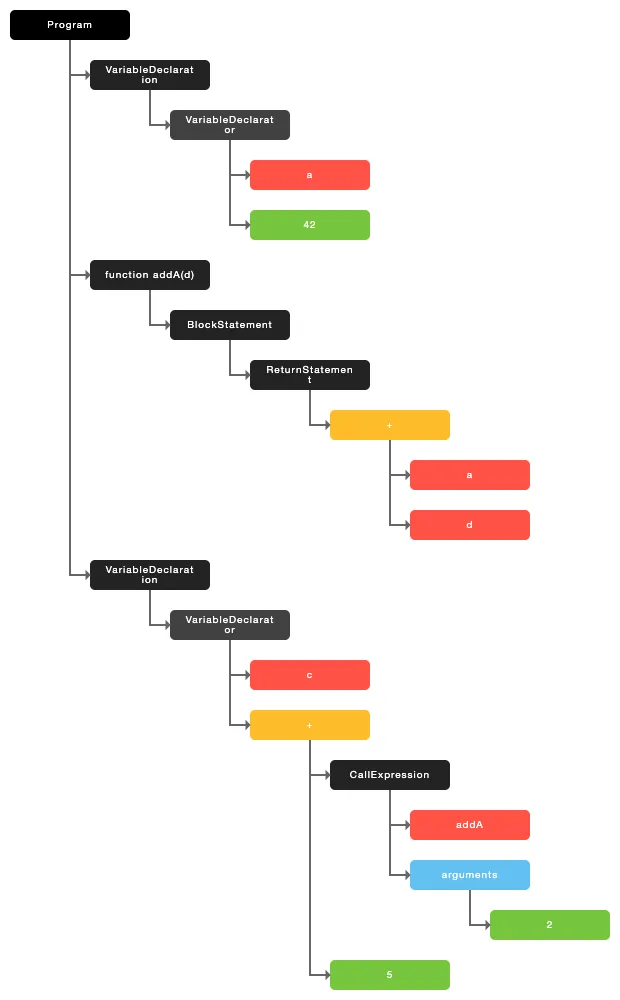
寫一個循環和遞歸，來一條條執行這些語法樹節點，一個解釋器就這麼憑空誕生了 🥳

這時候就有羣友要問了：語法樹有了，你的編譯器在哪裏？彙編在哪裏？你不要告訴我你可以在 CPU 裏面用 switch case！

😅：能跑就行，別催了，我還沒學到，下次一定

3️⃣ 解析數學式：玩弄字符串

到此爲止俺的編譯器旅程還是輕鬆愉快的，但是本文忽略了一個大問題……

怎麼構造那個樹狀結構❓❓

俺現在有一個字符串「1 + 31 * (5.5 + 2) - 4」，

要把這些文字轉換成樹狀結構，並且還要無視不同書寫格式導致的差異。
比如說，下面的 3 種寫法，都應該得到相同的結果：

// 1️⃣
1+31*(5.5+2)-4
// 2️⃣
1+   31  *(  5.5+ 2)  -4
// 3️⃣
1 + 3
1*(5.5+
2)-  // 這是註釋
4

這裏就需要一個能把字符串轉換成 token 的東西，就比如把上面那些亂七八糟的全部轉換成：

1 + 31 * ( 5.5 + 2 ) - 4

這樣類似一個字符串列表的數據結構，以便進一步分析。這個過程叫做「詞法分析」，所以編譯的第一步是寫一個詞法分析器（Scanner），並且至少要能區分數字，運算符號，括號等各個種類。

對於簡單的數學式計算，會用到下面這幾種 token：

enum TokenType {
  LEFT_PAREN, RIGHT_PAREN,
  DOT, MINUS, PLUS, SLASH, STAR,
  NUMBER,
  EOF
}

分類完 token，接下來就要正式開始了 😱
先欽定一下「形式語法」

expression     → term ;
term           → factor ( ( "-" | "+" ) factor )* ;
factor         → primary ( ( "/" | "*" ) primary )* ;
primary        → NUMBER 
               | "(" expression ")"

欽定了

表達式是一串加減式
加減式的左邊和右邊可以混合一串乘除式
乘除式的左邊和右邊必須是數字或者括號
括號裏面可以是表達式
表達式是一串加減式（套娃）

有了一組如同套娃的語法規則，就可以用「遞歸下降」算法來識別那些 token 並構造語法樹了。

1 + 31 * ( 5.5 + 2 ) - 4

遞歸下降是個有點小燒腦，🤯，的算法，如果妳有興趣，請務必移步 Crafting Interpreters，那邊有對人類友好的解釋。簡單來說，算法從第一個 token 開始，關注這一個和下一個 token，並往後掃描：

最開始是 1 和 +，說明這是加式
加式的左邊是 1，右邊是一個……語法規定，右邊是加減式或者乘除式
接下來是 31 和 *，說明這是乘式
乘式的左邊是 31，右邊是一個……語法規定，右邊不是乘除式就是數字或括號
右邊是個括號，語法規定，括號裏面是加減式
接下來是 5.5 和 +，說明這是加式，左邊是 5.5，右邊是……是個數字 2
所以第四步的乘式右邊是個括號加式
所以第一步的右邊是第七步的乘式

得到

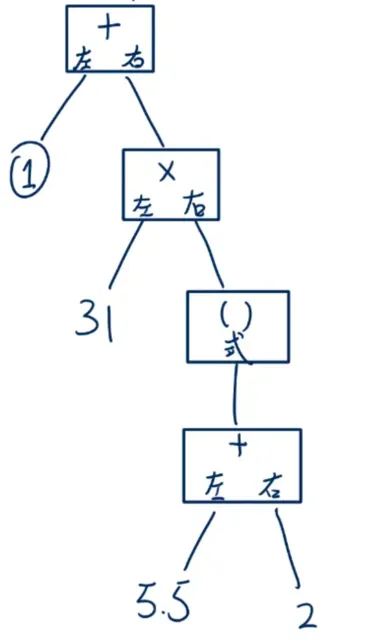
但是加減式是可以串聯的，俺們發現還剩一個 - 和一個 4，如法炮製，插入新的語法樹節點，最後就會得到本文一開始的語法樹了。

看起來很燒腦，實則一點都不容易，，，在構造語法樹節點的同時，還要注意檢測並報告不正確的語法，比如說，在循環外面 break 或者在函數外面 return。

俺花費了一個星期的 remote work 的空餘時間纔終於讓 Parser 跑起來。努力得到了回報，現在俺已經掌握了卡西歐計算器的核心科技了！

展望

我要大力感謝 Robert Nystrom 大大，他寫出了這麼好的書免費給我看 🥺
從開始學習到現在，俺花費了一個月，目前學到如何給語言增加面向對象的 Class 功能。

萬里長征，剛到一半 🥺

等我完成了所有語言功能，VM 的設計，就在前面！我已經迫不及待，😁，摩拳擦掌，👊🏻，準備要手撕一個自己的 VMProtect 出來了！

前輩們，我終將達到妳們的高度！
下次再見！

註釋

[1] 我自己。

[2] 手撕解釋器聖經 👉🏻 Crafting Interpreters

[3] 爛尾的 👉🏻 BGI引擎概論

[4] 語法樹製圖工具 https://www.jointjs.com/demos/abstract-syntax-tree